Ordinary Least Squares for Multiple Regression

II.II.1 OLS for Multiple Regression

The general linear statistical model can be described in matrix notation as

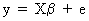
(II.II.1-1)

where y is a stochastic T*1 vector, X is a deterministic (exogenous) T*K matrix, b is a K*1 vector of invariant parameters to be estimated by OLS, e is a T*1 disturbance vector, T is the number of observations in the sample, and K is the number of exogenous variables used in the right hand side of the econometric equation.

It is furthermore assumed that

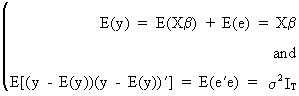
(II.II.1-2)

which is the equivalent matrix expression of the weak set of assumptions under section II.I.3.

The least squares estimator minimizes e'e (the sum of squared residuals).

Solving the normal equations X'Xb = X'y with respect to b yields

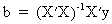
(II.II.1-3)

where X'X must be a non singular symmetric K*K matrix!

Obviously, the OLS estimator is unbiased

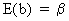
(II.II.1-4)

since E(X'e) = 0 by assumption (X is exogenous). This result can be proved quite easily. Note that if X is not exogenously given (thus stochastic) the small sample property of unbiasedness only holds if E(X'e) = 0.

Under the assumption of OLS it can be proved that the covariance matrix of the parameters is

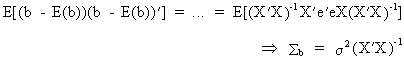
(II.II.1-5)

The Gauss-Markov theorem states that if

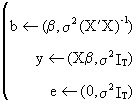
(II.II.1-6)

then any other estimator

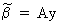
(II.II.1-7)

has a parameter covariance matrix which is at least as large as the covariance matrix of the OLS parameters

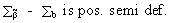
(II.II.1-8)

This important theorem therefore proves that the OLS estimator is a best linear unbiased estimator (BLUE).

If D^* is a K by T matrix which is independent from y and if

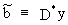
(II.II.1-9)

the parameter vector is by definition a linear estimator, and if

(II.II.1-10)

then it follows that

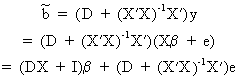
(II.II.1-11)

Evidently, it follows from (II.II.1-11) that the parameter vector can only be unbiased if DX = 0 and if E(D^*e) = 0.

Now what happens to the covariance matrix of this estimator? Obviously, we find

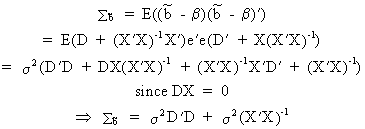
(II.II.1-12)

which proves the theorem (on comparing (II.II.1-12) with (II.II.1-5); Q.E.D.).

It can be proved that

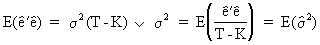
(II.II.1-13)

which states that the OLS estimator of the variance is unbiased.

The operational formula for calculating the variance is

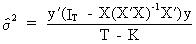
(II.II.1-14)

The prediction of y values outside the sample range is

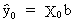
(II.II.1-15)

which is an unbiased prediction function

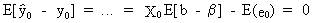
(II.II.1-16)

Example of extrapolation forecast

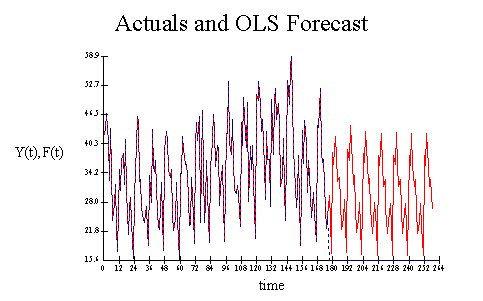
The point forecast error can be found as

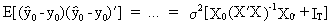
(II.II.1-17)

whereas the average forecast error is equal to

(II.II.1-18)

The degree of explanation can be measured by the determination coefficient (R-squared) or by the F-statistic which is defined as

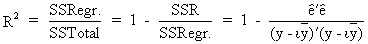
(II.II.1-19)

and

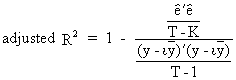
(II.II.1-20)

and

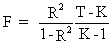
(II.II.1-21)

where the F statistic is valid for all ß coefficients except for the constant term.

To test the significance of a subset of m parameters (out of a total number of K) the following F test is used

(II.II.1-22)

which is in fact a generalization of (II.II.1-21).

The parameter estimation of a multiple and a simple regression are related to each other. It is also possible to prove that if all explanatory variables are independent (orthogonal), there is no difference between multiple and simple regression coefficients. Assume

(II.II.1-23)

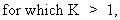
then it is easily deduced from (II.II.1-23) that any multiple regression parameter can be computed by

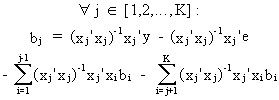
(II.II.1-24)

Since it is assumed that the explanatory variables are orthogonal it follows that

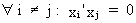
(II.II.1-25)

and due to the OLS assumptions we know that

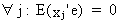
(II.II.1-26)

On substituting (II.II.I-25) and (II.II.1-26) into (II.II.1-24) we obtain

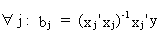
(II.II.1-27)

which proves the theorem (Q.E.D.).