Time Series Analysis - ARIMA models - Model Forecasting

V.I.4 Univariate Stochastic ARIMA Model Forecasting

The forecast (with forecast lead l) of a time series Y_t at a forecast origin t is denoted by F_t+l or F_t(l) which is, in our case, always a combination of previous observations.

The forecast can obviously also be written in terms of previous error-shocks

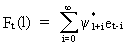
(V.I.4-1)

Remark that from (I.III-17) it follows that the forecast variance is

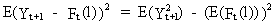
(V.I.4-2)

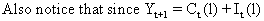
and due to (V.I.1-238) and (V.I.1-233) it follows that

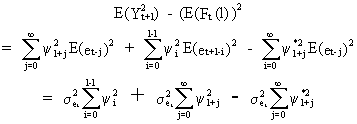
(V.I.4-3)

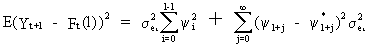
(V.I.4-4)

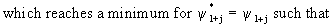
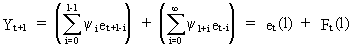
(V.I.4-5)

Hence, the forecast function (c.q. the conditional expectation of Y_t+l at t) is the minimum mean square error forecast. Also it is quite evident that the forecasts are unbiased since

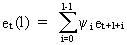
(V.I.4-6)

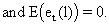
The variance of the forecast is equal to the first term of the RHS of (V.I.4-4). This illustrates why (V.I.1-51) (and especially the y-weights) can be used to compute the forecast confidence interval.

It is furthermore nice to see that the random innovations (c.q. shocks) are in fact equivalent to the one period ahead forecast error since

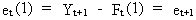
(V.I.4-7)

From (V.I.4-5) and (V.I.4-7) it follows that the one step ahead forecast errors are not correlated. Remark however that forecast errors for l > 1 are not uncorrelated.

There are two formulae for computing the correlations between forecast errors (l > 1): correlations between forecast errors at different origins with equal lead times, and correlations between forecast errors at equal origins with different lead times.

(Auto)correlations between forecast errors at different origins with equal leads are given by

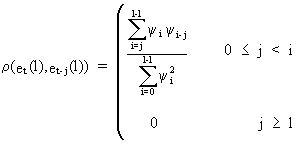
(V.I.4-8)

which can be easily proved on using

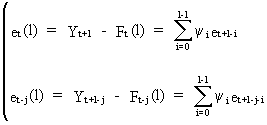
(V.I.4-9)

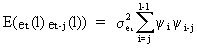
(V.I.4-10)

which proves (V.I.4-8) (Q.E.D.).

(Auto)correlations between forecast errors at equal origins but with different leads are given by

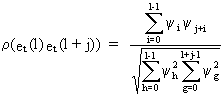
(V.I.4-11)

since

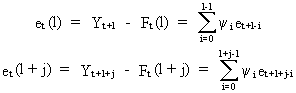
(V.I.4-12)

Hence, the covariance is

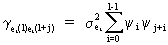
(V.I.4-13)

which, together with (V.I.4-12), proves (V.I.4-11) (Q.E.D.).

Forecasting of ARIMA(p,d,q) models

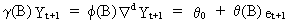
(V.I.4-14)

is straightforward since

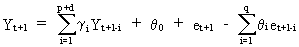
(V.I.4-15)

from which it follows that

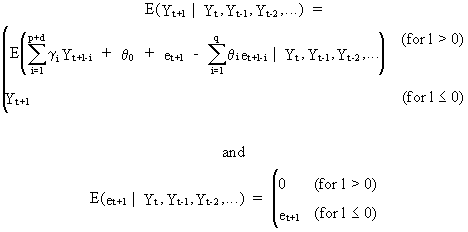
(V.I.4-16)

Eq. (V.I.4-15) provides a recursive forecasting algorithm which can be solved using a computer and a programming language able to perform recursions.

The forecast variances (and hence also the confidence probability limits) can be obtained from the y-weights.

These y-weights are computed from

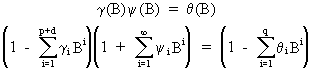
(V.I.4-17)

which can be used to equate coefficients of powers of B such that

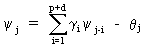
(V.I.4-18)

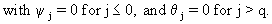
Remark that if j > max(p + d - 1, q) eq. (V.I.4-18) reduces to

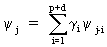
(V.I.4-19)

Sine the variance of the forecast is equal to the first term of the RHS of (V.I.4-4), it follows that

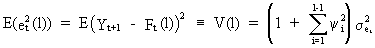
(V.I.4-20)

Confidence intervals can thus also be easily obtained.

Some explicit examples of the so-called eventual forecast functions are given in BOX and JENKINS (1976) and in MILLS (1990). These functions are used to study the fundamental nature of the forecasts. Since this goes beyond the scope of this work, and since the fundamental techniques of studying these forecast functions has already been given in previous sections, we only refer to the relevant literature.