II.I.1 The least squares criterion
There
are many techniques in econometrics and statistics that use the
least squares criterion. In regression techniques this criterion is
of immense importance.
Why
should a criterion be used at all? The answer to this question is
quite obvious: one has to have an objective measure for
discrepancies between the estimated values (generated by the
statistical model) and the (true) observed values. In fact we wish
to create mathematical models of our surrounding world in order to
be able to describe it, to draw conclusions from it, to forecast
future behavior of some (economic) phenomena, and to explain why
certain things happened in the past.
For
obvious reasons these mathematical models are not
deterministic but instead, probabilistic
or stochastic. This is the reason why we have a need for a good
criterion to decide whether our model does describe the real world
as good as possible.
Since
we cannot hope for a model to describe a real phenomenon perfectly,
the only thing we can do is to design a method for getting as close
to the real behavior as possible. This can be achieved by minimizing
the error of the mathematical model.
The
most obvious way to express the error made by a probabilistic model
is to calculate the sum of the deviations between the forecasted values and the real values:
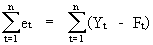
(II.I.1-1)
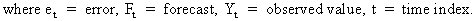
A
much better criterion is obtained when using the absolute
values of the deviations:
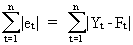
(II.I.1-2)
since
this will ensure that large positive errors are not compensated by
large negative errors.
Another
criterion can be defined by computing the
sum of squared deviations:
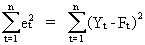
(II.I.1-3)
Using
the square of the deviations results in generating only positive
values (like in the previous criterion) but above that, it tends to
give more weight to large discrepancies in stead of small ones.
Remark
that eq. (II.I.1-3) is not always an improvement with respect to eq.
(II.I.1-2). This is because in some cases, where a very long
structural shift (in time) exists, the second criterion (II.I.1-2)
will describe specifically the long shift better than the third
criterion whereas the latter performs better in regard to overall
predictive power. Moreover, criterion (II.I.1-2) is more robust in the context of outliers.
From
now on we will always use the criterion of minimizing the Sum
of Squared Residuals (SSR) from equation (II.I.1-3), because
this criterion is most commonly used in econometrics. Above that,
the SSR criterion can be proved the be equivalent to another
important criterion (c.q. maximum likelihood) in certain
circumstances.
The
SSR criterion should never be confused with the Ordinary
Least Squares technique (OLS)! In fact, OLS does use the SSR
criterion but so do a lot of other techniques like for instance
Multiple Stage Least Squares, Weighted Least Squares, Generalized
Least Squares, the Maximum
Likelihood Estimation (MLE) under certain conditions, etc...
| 
