Time Series Analysis - ARIMA Models - Wold decomposition theorem

Wold's decomposition theorem

The most fundamental justification for time series analysis (as described in this text) is due to Wold's decomposition theorem, where it is explicitly proved that any (stationary) time series can be decomposed into two different parts. The first (deterministic) part can be exactly described by a linear combination of its own past, the second part is a MA component of a finite order.

A slightly adapted version of Wold's decomposition theorem states that any real-valued stationary process Y_t can be written as

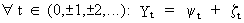
(V.I.1-171)

where y_t and z_t are not correlated.

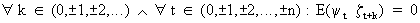
(V.I.1-172)

where y_t is deterministic

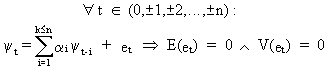
(V.I.1-173)

and

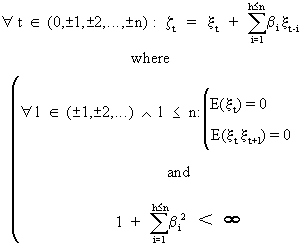
(V.I.1-174)

(z_t has an uncorrelated error with zero mean).

Because of its importance for time series analysis in general, and in practice, we will discuss the proof of Wold's decomp. theorem shortly.

Since there seems to be much confusion in literature about this theorem, we will only discuss the proof of another version (than that described above) which can be proved quite easily. In order to make a distinction with the previous description, we will explicitly use other symbols.

Denote a stationary time series W_t with zero mean and finite variance.

In order to forecast the time series by means of a linear combination of its own past

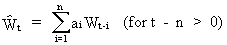
(V.I.1-175)

a criterion is used to optimize the parameter values. This criterion is

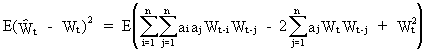
(V.I.1-176)

which is called the sum of squared residuals (SSR).

The normal equations (c.q. eq. (V.I.1-176) differentiated w.r.t. the parameters) is easily found to be

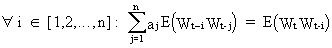
(V.I.1-177)

In matrix notation eq. (V.I.1-177) becomes

(V.I.1-178)

with

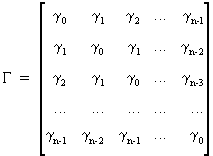
(V.I.1-179)

which is symmetric about both diagonals due to the stationary of W_t and with

(V.I.1-180)

On adding an error component e_t,n to eq. (V.I.1-175) it can be shown that

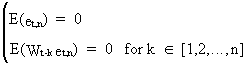
(V.I.1-181)

The first part of (V.I.1-181) is almost trivial

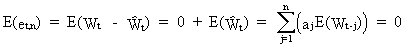
(V.I.1-182)

The second part of (V.I.1-181) is

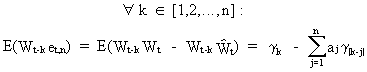
(V.I.1-183)

with a RHS equal to zero since the parameters satisfy (V.I.1-177) (Q.E.D.).

On repeating the previous procedure we obtain

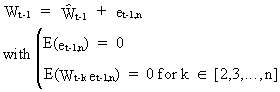
(V.I.1-184)

Remark that the error components (V.I.1-181) and (V.I.1-184) are uncorrelated due to (V.I.1-181), from which we obviously find

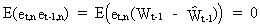
(V.I.1-185)

On substituting (V.I.1-184) into (V.I.1-175) it is obvious that

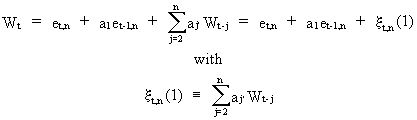
(V.I.1-186)

where x_t,n(1) depends on the past of W_t-1

Also it is obvious from (V.I.1-183) that

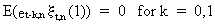
(V.I.1-187)

and from (II.II.1-27) and the fact that e_t,n is independent from the other regressors of (V.I.1-186), that

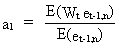
(V.I.1-188)

On repeating the step described above it is easy to obtain

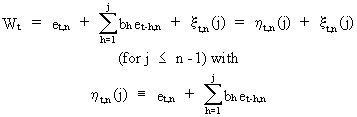
(V.I.1-189)

with

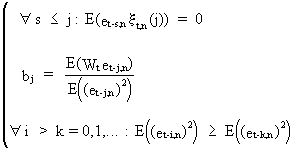
(V.I.1-190)

On applying (V.I.1-189) and (V.I.1-190) on W_t-i we obtain

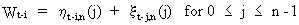
(V.I.1-191)

where x_t-i,n always depends on it's own past only, and where evidently

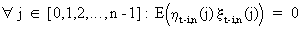
(V.I.1-192)